Research

As a research scientist, I’m currently interested in theoretical aspects of gravity and quantum information science; particularly on how quantum computers can be benchmarked using quantum gravity.

Earlier in my graduate career, I worked on various aspects of the classical, semiclassical, and quantum properties of black holes. Some of my projects are highlighted below.

Quantum Gravity $\textit{\&}\ $ Holography

I have a long history of being involved in studying aspects of quantum gravity via holography. Holography, also referred to as AdS$_{d+1}$/CFT$_{d}$ or as the gauge/gravity duality, is a collection of ideas which form a toolkit. The toolkit allows one to convert difficult problems in a type of quantum field theory, known as conformal field theory (CFT$_{d}$), into simpler problems encountered by gravity theories with a negative cosmological constant, called anti de Sitter gravity (AdS$_{d+1}$). One condition to use the toolkit is that the conformal field theory operates in $d$-dimensions whereas the gravity theory lives in one dimension higher, i.e., $d+1$-dimensions.

Earlier in my academic career, I used gravity to model aspects of nuclear physics and the theory of strong interactions, QCD -- which behaves like a CFT$_d$ at high energies. Recently, I have turned my attention to using CFT$_d$ to answer problems in gravity through the holographic toolkit. Along this line, my current research interests are entanglement entropy, lower dimensional gravity, and black hole information.

Deforming CFT$_d$ and the Hawking-Page Transition

In my most recent paper on holography, my collaborator and I established a new result on the Hawking-Page transition in AdS$_{d+1}$ gravity and its relationship to the deconfinement/confinement phase transition found in certain CFT$_{d}$. Like the phase transition where ice melts into water at high temperatures, composite particles, such as protons and neutrons, also melt at high temperatures into a quark-gluon plasma. When a phase transition occurs in the CFT$_d$ side, holography tells us that a black hole is expected to spontaneously form from a collapse of thermal gas in the AdS$_{d+1}$ side. The spontaneous formation of black holes at a critical temperature $\beta$ is known as the Hawking-Page transition.

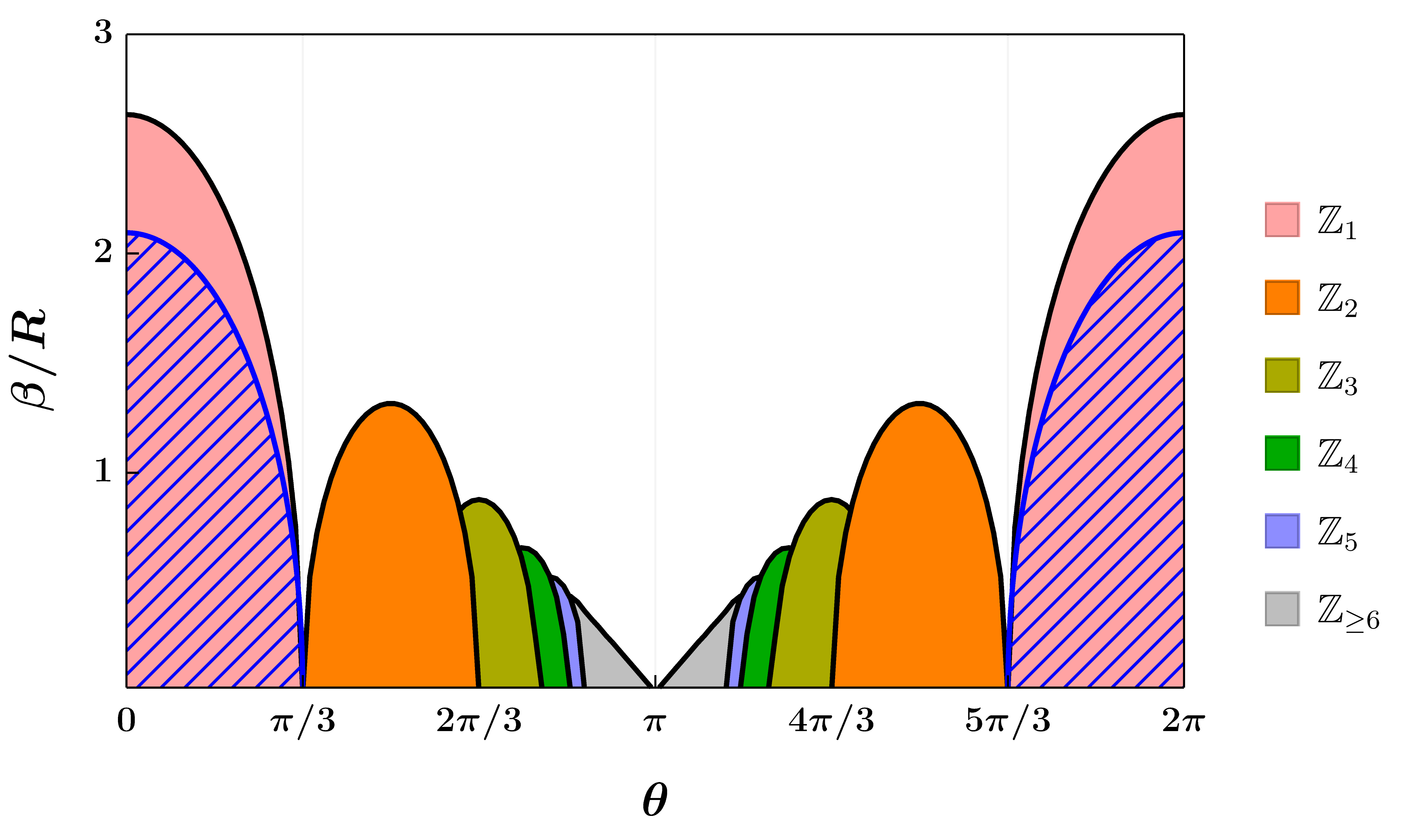
In an earlier paper by Edward Witten , it was observed that the deconfinement/confinement phase transition can be avoided by deforming the CFT$_d$ side. In such cases, it was conjectured that black hole formation is prohibited in such cases. We asked a simple question; Is this conjecture true, and if so, when this phase transition is avoided, is the formation of black holes suppressed abruptly or continuously? This is a sharp quantum gravity question we can answer via the holographic duality. Our construction uses a parameter $\theta$ which controls the phase transition. The results are highlighted in the right figure. We found that the phase transition (the filled regions) is avoided at $\theta=\pi/3,\pi,5\pi/3$ whereas the black hole formation (the hatched region) is prevented whenever $\theta\in[\pi/3,5\pi/3]$.

The result is surprising for several reasons. We expected black hole formation to be suppressed abruptly but it appears that black holes can still form for a small window! Secondly, there are mismatchs - there are missing islands and the temperatures $\beta$ do not precisely match up at $\theta=0$. It is always exciting to encounter such mismatches as they inspire deeper questions about the nature of gravity in holography that I am currently investigating!

Uniform Black String Instabilities in Anti de Sitter

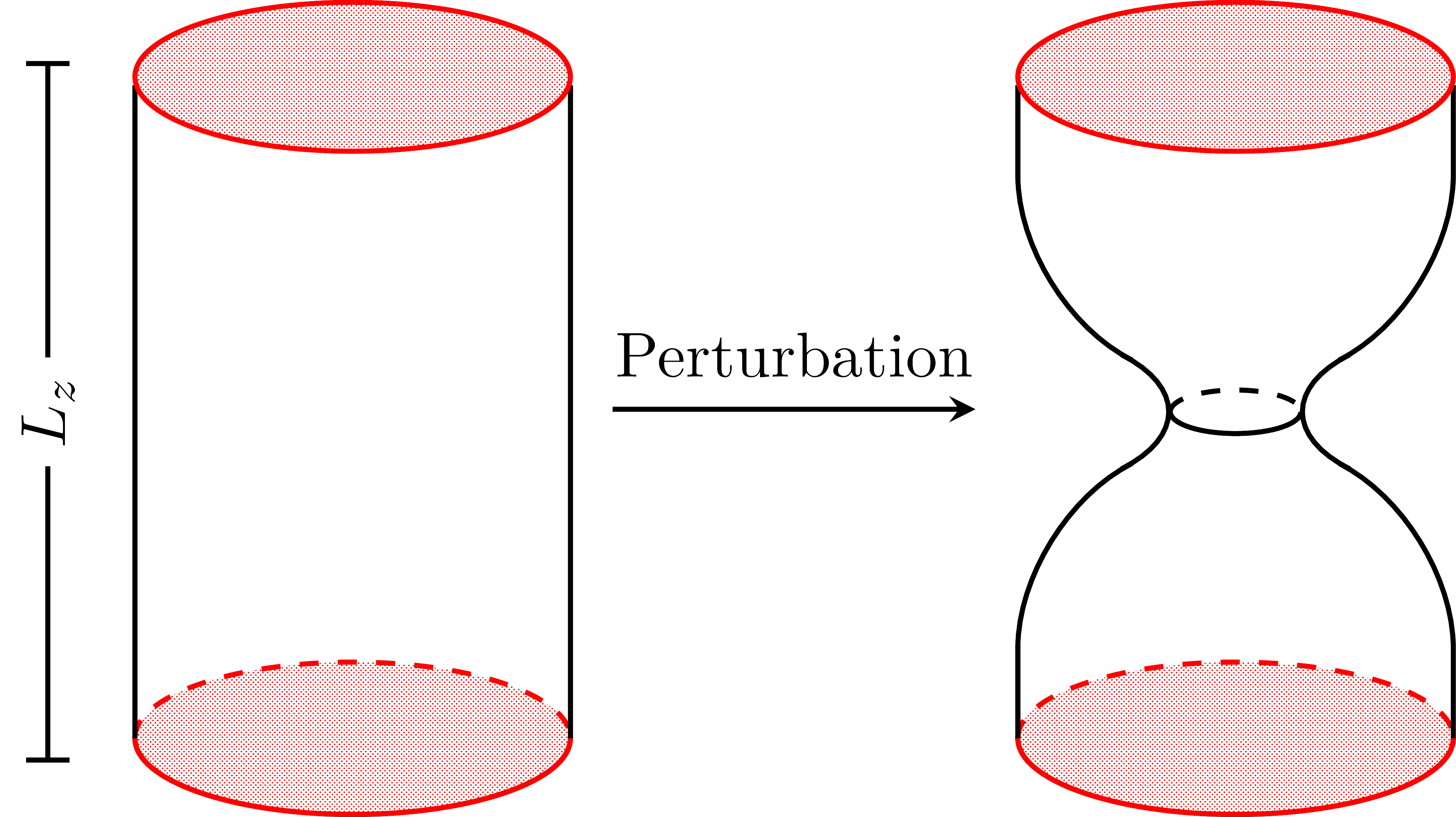
In 2021, my collaborator and I showed that uniform black strings in AdS (AdS UBS) suffer from the Gregory-Laflamme instability; an instability which causes black string objects to develop a pinch in their horizons (shown in the left cartoon). At the end state of the instability, a singularity is expected to appear and the black string fragments into two black holes.



It was previously suspected that the AdS UBS could avoid the instability. However, we performed a numerical search for the instability and found a parameter regime where the instability can occur (shown in the below images in $d=5,\dots,9$ on the left and $d=10$ on the right).

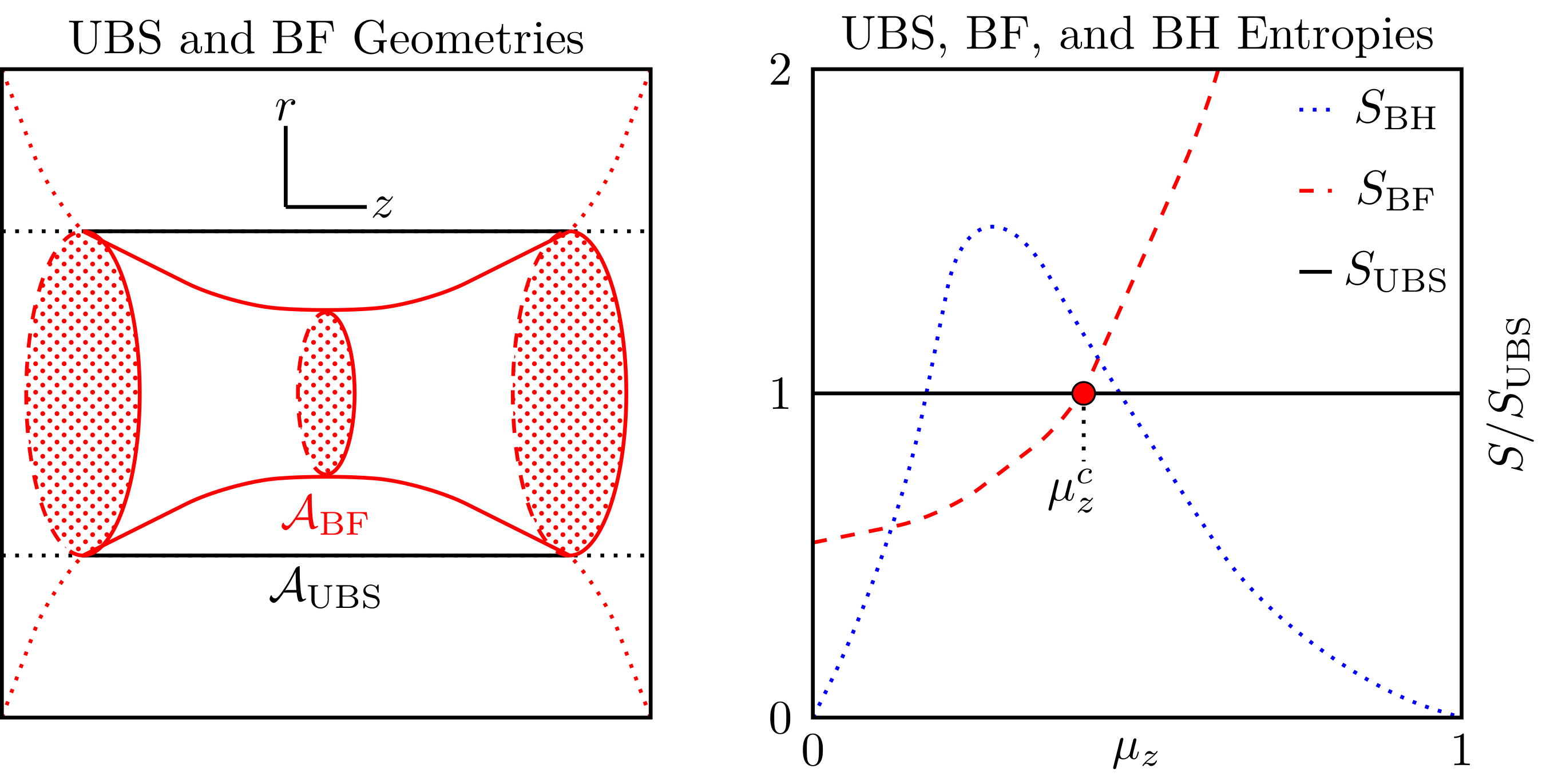
If the conditions are just right, a black string will fragment into several smaller black holes at the end state of the GL instability. The transition between uniform black strings and black holes (BH) are interesting as a naked singularity is formed in finite time. However, if certain conditions are not met, the BS will instead converge onto different geometry without a naked singularity forming. In this paper, we argued that the AdS UBS could either fragment into a BH or converge onto a black funnel geometry (BF). We found conditions where the fragmentation is more likely (i.e., entropically favorable) rather transitioning smoothly to a BF state.