The [[5,1,3]] Stabilizer Code

Quantum computers built with physical qubits are susceptible to propagation of error due to either decoherence, thermal, or other quantum noise thereby lowering the trust in the computational output. One clever (but computationally expensive) way around this is to devise special codes which not only produce high fidelity results even if a few errors accumulate but also have a clear syndrome which encodes the type of error that occurred and its location.

One such famous code is the five qubit error correcting code. In this code, five physical qubits are arranged in such a way that they encode a single logical qubit $|\psi\rangle$. Then any single qubit error, such as a bit or phase flip error, does not disturb (much) the logical information stored in $|\psi\rangle$. Furthermore, there is a clear diagnostic, namely the syndrome, which can be extracted from the code and used to determine what the error type is and where the error occurred in order to correct it. In this way, the five qubit error correcting code protects a single logical qubit from any single physical qubit error.

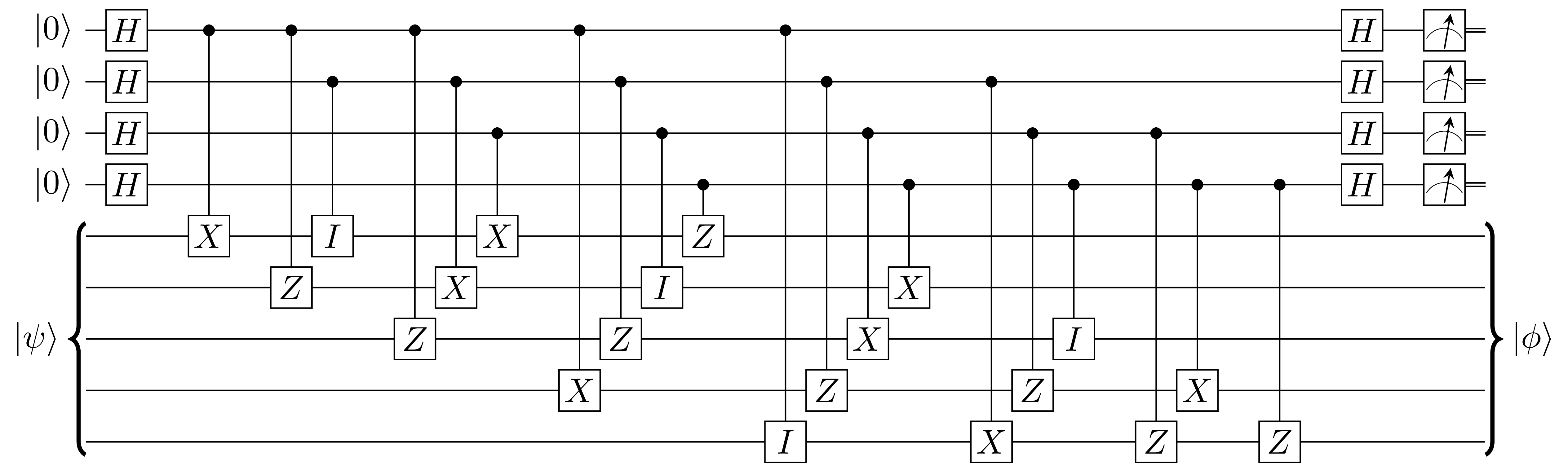
To be more concrete, let’s code up the $[[5,1,3]]$ stabilizer code in Mathematica. The circuit is split into two parts; the top four registers are ancillas where as the bottom register $|\psi\rangle$ is the logical qubit. The gate set $(H,X,Z,I)$ are the usual Hadamard, Pauli X and Z, and the identity. The generators $\mathcal{G}$ are given by cyclic permutations of the following stabilizer $S = (XZZXI)$, i.e., $$ \mathcal{G} = (XZZXI, IXZZX, XIXZZ, ZXIXZ) $$ and the logical operators are $\bar{X}=XXXXX$ and $\bar{Z}=ZZZZZ$. The fifth cyclic permutation is omitted since it can be expressed as a linear combination of the other generators. In Mathematica, set

S1 = {X, Z, Z, X, Identity}

then the stabilizer set is given by

Stabilizers = Table[RotateRight[S1, i], {i, 0, Length[S1] - 2}]

These stabilizers are encoded into the registers associated with the logical qubits and are linked correspondingly to the ancilla. If an error occurs in the logical qubit, say an $X$ error on the first register in $|\psi\rangle$ corresponding to the error operator $E_X=XIIII$, then one can check that $[E_X,\mathcal{G}_ a] \propto \delta_{a4}$ implying that the error commutes with all stabilizers except for $ZXIXZ$. Hence, the corresponding syndrome associated with this error will be $0001$. To correct this error, we simply need to apply another $E_X$ to the same register.

To introduce these stabilizers at the appropriate site location within the logical qubit and to link appropriately with the ancilla, assign to each qubit an index $i=1,\cdots,9$. Then the site locations are given by

Sites = Partition[
  SortBy[Flatten[Table[{i, 4 + j}, {i, 1, 4}, {j, 1, 5}], 1], Total], 
  5]

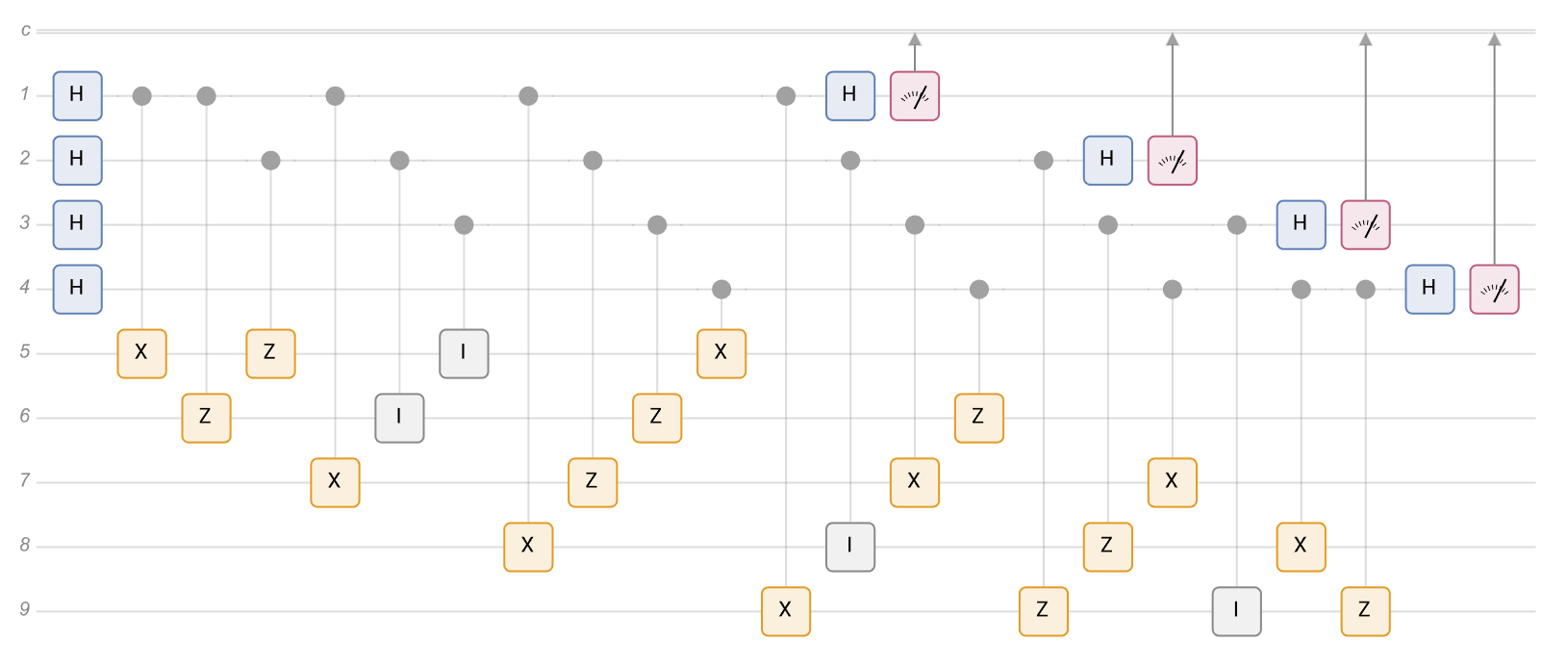
Now, we are ready to design the circuit. We do this as follows. The top four registers are acted upon a Hadamard. Then the full set of stabilizers are encoded into the register corresponding to the logical qubit at the site locations described above. The last step is to again act on the ancillas with Hadamards and then measure to see if any errors have occurred. The circuit is shown below!

QECC5 = Flatten[
   Join[Table[QuantumOperator["Hadamard", {i}], {i, 4}], 
    Table[Table[(QuantumOperator[{"Controlled", 
         ToString[Stabilizers[[j, i]]]}, Sites[[j, i]]]), {i, 
       Length[Stabilizers[[1]]]}], {j, Length[Sites]}], 
    Table[QuantumOperator["Hadamard", {i}], {i, 4}], 
    Table[QuantumMeasurementOperator[{i}], {i, 4}]]];
Show[QuantumCircuitOperator[QECC5]["Diagram"], ImageSize -> Full]

The complete Mathematica notebook can be found here.