Information Loss via Ricci Flow

When I was in New York City for the Quarks2Cosmos APS April Meeting this year, I was chatting with some friends about black hole evaporation, where black holes evaporate away due to quantum effects near their apparent horizon thereby violating unitarity in quantum mechanics. The phenomenon is at the heart of many developments in modern theoretical physics and was one of my primary inspirations to study the information loss problem earlier in my career. This process of evaporation is effectively encoded in the semi-classical Einstein equations $$ G _{ab} + \Lambda g _{ab} = {8\pi G _{\rm N}}\left\langle{\hat{T} _{ab}}\right\rangle _{\psi} $$

where classical gravity arising from a Lorentzian metric $g_{ab}$ is coupled to the expectation value of a quantum stress-energy operator $\left\langle{\hat{T} _{ab}}\right\rangle$ acting on some predefined global quantum state $\psi$. For certain geometries and quantum matter, the backreaction of quantum effects near the horizon causes the black hole surface area to shrink.

The connection between black hole evaporation and information loss comes from the Bekenstein-Hawking entropy formula $$ S _{\rm BH} = \frac{\mathcal{A} _{\mathcal{H}} }{4 G _{\rm N}} $$ where $\mathcal{A} _{\mathcal{H}}$ is the surface area of the black hole with an event horizon $\mathcal{H}$ and $S _{\rm BH}$ is the thermal entropy required to construct such a black hole. Hence, black hole evaporation is identical to information loss if one interprets $S _{\rm BH}$ as an information measure.¹

Here, I discuss the Ricci flow, introduce the Fisher information, and describe the loss of Fisher information via Ricci flow. As a bonus, there are nice bounds that one can construct and I wrap things up by contrasting information loss via Ricci flow against information loss from black hole evaporation.

The Fisher Information #

One of the early joys of Perelman’s work is that Ricci flow admits a gradient flow or variational reformulation. The setup is as follows, for closed Riemannian manifolds equipped with a metric and a scalar field $(\Sigma,\gamma,\Phi)$, consider the Fisher information (or the CGHS model without additional matter in $d$ dimensions) given by $$ \mathcal{F}_ \Sigma = \kappa\int_\Sigma (R+ \gamma^{ab}\partial_ a\Phi\partial_ b\Phi)e^{-\Phi}\sqrt{\gamma} d^dx,\ \ \ \ \kappa = \frac{1}{16\pi G_ N} $$ One can embed $\Sigma$ as an initial data hypersurface in a Lorentzian spacetime with metric $$ ds^2 = -N(x^a)dt^2 + \gamma_{ab}(t) dx^a dx^b $$ thereby promoting the Fisher information stored in the initial data surface $\Sigma = \Sigma_ {t=0}$ to a time-dependent quantity $$ \mathcal{F}(t) \equiv \mathcal{F}_ {\Sigma_ t} =\kappa \int_ {\Sigma_ t}(R_t + \gamma_t^{ab}\partial_ a\Phi\partial_ b\Phi)e^{-\Phi}\sqrt{\gamma_ t}d^d x. $$

To show that the Ricci flow emerges as a gradient flow of the Fisher information, we need to consider an extremization problem subject to the following constraint: $$ \partial_ t\tilde{\mu}[\Sigma] = \frac{\partial}{\partial t}\int_{\Sigma_t}e^{-\Phi }\sqrt{\gamma_t} d^d x = 0 $$ Now a quick calculation shows that the Fisher information has the first variation $$ \partial_ t \mathcal{F}(t) = -\kappa\int (R_ {ab} + \nabla_ a\nabla_ b \Phi) \partial_ t\gamma^{ab} e^{-\Phi}\sqrt{\gamma_ t} d^{d}x $$ From here, we can see that if we had a solution to the following flow $$ \partial_ t \gamma_{ab} = - 2\ell (R_ {ab} + \nabla_ a\nabla_ b\Phi)\newline {\partial_ t\Phi} = {\partial_ t \sqrt{\gamma}} $$ (which is just the dimensionally consistent Ricci flow in disguise, see Topping Section 6) subject to the constraint $\partial_t \tilde{\mu} = 0$ then the Fisher information would evolve monotonically. Concretely we have the theorem

Theorem: Monotonicity of Fisher Information #

Now, this is quite nice! It seems that there is a appropriate information measure which behaves nicely under the Ricci flow discussed above. In fact, one can do much better. It turns out that the growth of the (subtracted or normalized) classical Boltzmann-Shannon entropy provides the following bound on the Fisher information, $$ \partial_ t \mathcal{F} \ge \frac{2}{d\ell} \mathcal{F}^2. $$ This is a resource if one wants to construct sharper bounds on geometric quantities.

The Area Growth Bound #

The proof techniques involved in utilizing Ricci flow to establish the monotonicity of the Fisher information (or the CGHS model) is essential prove a growth bound on ${\rm Area}(\Sigma_ t)$.

The essence of the argument boils down to the constraint imposed on the conformal volume measure $$ \tilde{\mu}[\Sigma] = \int_{\Sigma_ t}e^{-\Phi} \sqrt{\gamma_ t} d^dx $$ to formulate the Ricci flow as a gradient flow. Physically, the reason for the condition $\partial_ t\tilde{\mu}[\Sigma]=0$ on the conformal volume measure is introduce some control on how quickly the volume (or area) can increase under the flow. But essentially this can be leveraged to provide a bound on the growth of the actual volume measure on $\Sigma_ t$ defined by $$ {\mathcal{A}[\Sigma_ t] = \int_ {\Sigma_ t} \sqrt{\gamma_ t}d^d x} $$ This is the main player in the following analysis and the remaining calculation is to ascertain a bound on its growth. Henceforth, I refer to this quantity as the area of $\Sigma$.

The Einstein-Hilbert Action and Area Growth #

We can directly check the variation of $\mathcal{A}[\Sigma_ t]$, we have $$ \partial_t \mathcal{A}[\Sigma_ t] = \int_{\Sigma_ t}\partial_t \sqrt{\gamma_ t}\ d^dx. $$ A common identity in Riemannian (and even Lorentzian) geometry is that variations in the measure can be recast in terms of the metric $$ \partial_ t \sqrt{\gamma_ t}= \frac{\sqrt{\gamma_t}}{2}\gamma^{ab}(t)\partial_ t\gamma_ {ab}(t) $$ At this stage, we can use up the result from the analysis of the Fisher information, namely that $$ \gamma^{ab}\partial_ t\gamma_ {ab} = -2\ell (R + \Delta\Phi ) $$ then the right hand size becomes $$ \partial_ t\sqrt{\gamma_ t} = -\ell(R + \Delta \Phi)\sqrt{\gamma} $$

Hence, applying these formulas, the growth of the area is $$ \begin{align*} \partial_ t\mathcal{A}[\Sigma_ t] &= - \ell \int_ {\Sigma_ t}(R+\Delta \Phi)\sqrt{\gamma_ t}d^dx\newline &= -\ell\int_ {\Sigma_ t}R \sqrt{\gamma_ t}d^dx \end{align*} $$ where I have integrated away $\Delta \Phi$ as there is no boundary.

Remarkably, the preservation of the conformal volume measure along the Ricci flow gives us that the area growth of $\Sigma$ is precisely the action for classical gravity, i.e., the Einstein-Hilbert action. Clearly, there are additional boundary contributions when $\Sigma$ is not closed as I have been assuming throughout this article. However, for the manifolds under consideration thus far, we have the following theorem

Theorem: The Boundedness of Area Growth #

Although this is the central result of this post, one cannot make further headway unless an explicit form or at least symmetry is provided for the metric $\gamma_{ab}.$ Next I’ll briefly review some monotonicity bounds in the context of maximally symmetric spaces and ADM spaces.

Maximally Symmetric Spaces #

For maximally symmetric spaces, one has that $R_ {ab} = (2/d)\Lambda \gamma_ {ab}$ where $\Lambda\in\mathbb{R}.$ For these manifolds, the area growth can be shown to satisfy the differential equation $$ \partial_ t \mathcal{A}[\Sigma_ t] = - 2\Lambda \ell \mathcal{A}[\Sigma_ t] $$

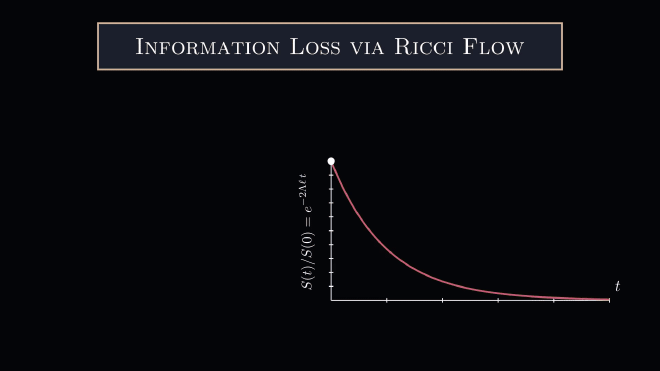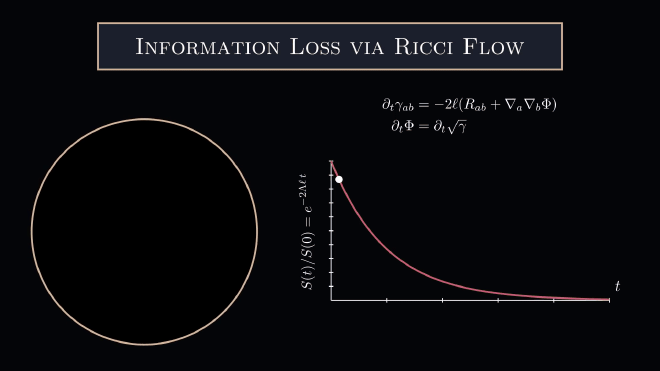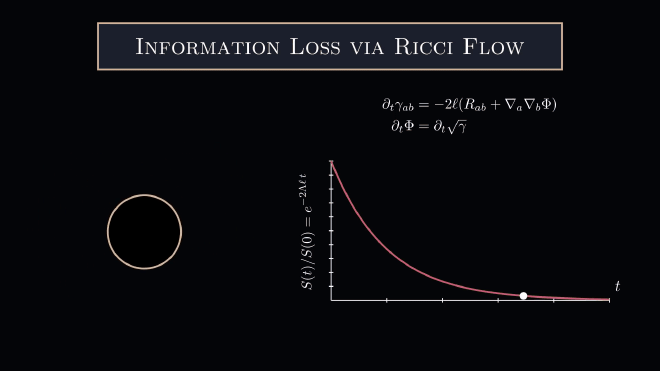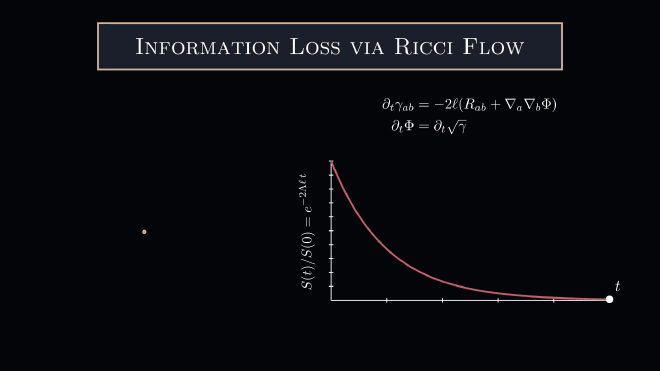
which has the general solution $$ \mathcal{A}[\Sigma_ t] = \mathcal{A}[\Sigma_0]\exp(-2\Lambda\ell t). $$

The coefficient in the exponent gives us a measure on the growth rate of the area. Here, the length parameter is naturally set by the radius of the sphere $(\Lambda>0)$, hyperbolic space $(\Lambda<0)$, or the periodicity of the torus $(\Lambda=0)$. For maximally symmetric spaces, the area growth saturates all inequalities, since $$ |\partial_t\mathcal{A}[\Sigma_t]| = |2\Lambda\ell|\mathcal{A}[\Sigma_t] =\mathcal{R}\mathcal{A}[\Sigma_t] $$

Lyapunov Exponents, and Entropy Production #

In addition to being associated with the absolute scalar curvature, there is another natural interpretation afforded to the growth coefficient, namely that

In the context of dynamical systems, the Lyapunov spectrum is used to estimate the rate of entropy production. It is quite tempting to characterize this entropy production in the context of black hole information. Indeed, the Bekenstein-Hawking formula conjectures that the entropy of a black hole is proportional to the surface area of the black hole. Applying this conjecture here for a spherically symmetric space, one finds that a spherical shell of radius $\ell$ with the initial metric $$ ds^2_ {\Sigma} = \ell ^2ds^2_{\mathbb{S}^d},\ \ \ \ \ \ \Lambda_{\rm sph} = \frac{(d-1)}{\ell^2} $$ has an exponentially decreasing entropy $$ S(t) = \frac{\mathcal{A}[\mathbb{S}_ t^d]}{4G_ N} = S_ {\mathbb{S}^d} \exp\left(-\frac{2(d-1)}{\ell} t\right). $$ In the language of dynamical systems, the spherical spaces have a negative Lyapunov exponent $\lambda_{\rm Lya.}<0$ and therefore are dissipative/shrink under the Ricci flow. Note that the entropy loss is quick at early times and slow at late times.

Entropy Loss in Canonical Ricci Flow #

In fact, independent of the calculation presented here, it is known that a sphere collapses linearly under the canonical Ricci flow in finite flow time (see Topping, Perelman, and Tao). For spheres, the canonical Ricci flow yields $$ \begin{align*} ({\rm Canonical\ RF})\ \ \ \partial_t\gamma_{ab} &= -2\ell R_{ab} = -\frac{4\ell \Lambda}{d} \gamma^i_{ab} \end{align*} $$ Solving this differential equation, it is clear to see that $$ \begin{align*}\gamma_{ab}(t) &= \left(1-\frac{4\ell\Lambda}{d}t\right)\gamma_{ab}^i\newline \implies S_{\rm canon}(t) &= S_{\mathbb{S}^d}\left(1-\frac{4\ell\Lambda}{d}t\right)^{d/2} \end{align*} $$ Unlike the Ricci flow with the conformal volume constraint, the collapse of the sphere is finite $$ t_{\rm collapse} = \frac{d}{4\ell \Lambda}. $$ In our case, the exponential collapse is due to the conformal volume constraint.

Comments on Black Hole Evaporation #

This entropy loss due to Ricci flow for spheres is analogous to the entropy loss of a Schwarzschild black hole in the semiclassical regime. But one should be cautious when making this comparison.

1. Foremost, the Ricci flow is not relativistic since $1^{st}$ order in coordinate time. It is much more analogous to the Heat/Schroedinger equation as schemeatically one has $$ \partial_t \gamma_{ab} = f_{ab}(\partial^2\gamma,(\partial\gamma)^2) $$ whereas Hawking evaporation takes place on a relativistic arena.

2. Secondly, given that $S_{\rm Sch}(t) = \mathcal{A}/4G_ N\propto r_+^{d-1}$ and $M_ {\rm Sch} \propto r_ +^{d-2}$, and assuming that the black hole can be taken to be a perfect blackbody, one finds that the mass loss gives $$ \frac{\partial M}{\partial t} \sim -\frac{1}{M^2} \implies S_{\rm Sch}(t)\propto S_{\mathbb{S}^d}\left(1-\frac{t}{t^\prime_{\rm collapse}}\right)^{(d-1)/{3(d-2)}}. $$ This is certainly qualitatively different to the entropy loss due to Ricci flow when the conformal volume is preserved. Whereas the Hawking evaporation picture seems to predict total entropy loss in finite time, the Ricci flow subject to a conformal volume constraint leaves an infinitely slow decaying remnant.

3. Hawking radiation is expected to evaporate black holes in spacetimes with any asymptotics. However, the conformal volume preserving Ricci flow generates entropy $\Lambda<0$ or is unchanged in flat space $\Lambda=0$ which is in tension with what we know from quantum field theory in curved spacetime with Minkowski asymptotics.

However, it is interesting to note the canonical Ricci flow is much more similar to Hawking evaporation, which raises the question

For what Ricci flow does one obtain the same entropy loss profile?